Je peste assez souvent sur le fait que, en cours de maths ou de science, ou même lors des formations professionnelles, l’on nous crache des formules sur un tableau que l’on doit ensuite copier sur un cahier et ressortir en contrôle, puis faire trois ou quatre applications numériques pour « montrer qu’on a bien compris ».

Sauf qu’appliquer une formule littérale en y injectant des valeurs numériques, ce n’est n’est pas « comprendre la formule » et la physique sous-jacente. C’est comprendre le principe d’une formule quelconque, c’est tout.

Un exemple simple : l’énergie électrique consommée, c’est égale à la puissance produite multipliée par la durée de production. La puissance s’exprime en kilowatts, et la durée en heures. L’énergie étant le produit des deux, c’est pour cette raison que l’énergie s’exprime habituellement en kilowatt⋅heures, c’est à dire des kilowattheures.
Inversement, si l’on divise une énergie consommée par une durée, on divise des kilowattheures par des heures, et on se retrouve avec des kilowatts, une puissance. La puissance est donc un débit d’énergie.

Toutes les formules en sciences ont une logique comme ça.

Autre exemple : si une grandeur dans une formule se trouve au numérateur, et qu’elle augmente, elle augmente aussi ce qu’on cherche à calculer. Si la même grandeur est au dénominateur, son augmentation diminue notre résultat ! Trivial quand on le sait, mais compliqué pour beaucoup.
Pourquoi ? Parce que c’est tellement trivial qu’on ne l’enseigne pas, ou bien qu’on n’insiste pas dessus avec une l’importance qui s’impose.

Dans l’autre sens, maintenant, quand on a un ensemble de grandeurs que l’on sait reliées par une formule que l’on a oublié, on peut prendre chaque grandeur et voir ce qu’elle fait sur le résultat : si elle l’augmente ou la diminue, on peut savoir s’il faut la mettre au numérateur ou au dénominateur respectivement.

Dès l’instant où l’on a un minimum d’intuition sur l’action des grandeurs entres elles, on retrouve assez facilement les formules pour peu qu’elles soient assez simples.
Pour les formules plus complexes, avec des racines ou des exponentielles, on peut utiliser l’outil très puissant de l’analyse dimensionnelle.
En résumé, des outils existent pour retrouver n’importe quelle formule physique simplement avec la liste des grandeurs qui doivent s’y trouver.

Ça c’était l’intro.

Si j’en parle c’est pour ce qui suit.

Récemment je discutais avec quelqu’un qui posait la question de savoir combien il y a de combinaisons possibles sur un cadenas à 3 chiffres. Vous pouvez essayer en posant la question autour de vous : normalement, tout le monde tombe dans le piège et dira « 999 », là où la réponse est 1 000, car il ne faut pas oublier la combinaison 000, en plus des neuf cent quatre-vingt-dix-neuf autres de 001 à 999.

Si cadenas dispose de 3 disques et que chaque disque permet de choisir un chiffre parmi 10, alors le nombre de combinaisons est 10 à la puissance 3, soit 10³.
Plus généralement, avec N disques de M valeurs, alors le nombre de combinaisons possibles est M^N.

La personne avec qui on s’amusait sur ces calculs se souvenait d’une formule avec des factorielles. Je m’en souvenais aussi, mais quelle était cette formule ? Comment la retrouver ?

Sur un cadenas à 3 disques de 10 chiffres, le nombre de combinaisons est bien 10³. Pas de factorielles ici. La raison est que chaque disque a autant de chiffres et que on peut réutiliser plusieurs fois le même chiffre.

À l’inverse, si on avait un cadenas qui interdisait d’avoir plusieurs fois le même chiffre, le formule n’est plus 10×10×10, mais plutôt 10×9×8. La raison est que l’on a 10 choix sur le premier chiffres, mais une fois qu’on a choisi le premier, le second chiffre n’a plus que 9 choix, vu que l’on s’interdit de prendre le chiffre du premier disque. Pour le troisième disque, on s’interdit les chiffres des deux autres disques, d’où seulement 8 possibilités restantes. Le nombre de combinaisons est donc 10×9×8, soit 720.

On remarque ici que 10×9×8, c’est le début de l’expression d’une factorielle : en effet, 10! = 10×9×8×7×6×5×4×3×2×1.

Comme il nous faut seulement le 10×9×8, on peut prendre 10! et le diviser par 7!, c’est à dire 7×6×5×4×3×2×1. Ainsi, il ne restera effectivement que 10×9×8 lorsque l’on simplifie. La formule pour un cadenas où chaque chiffre doit être unique est donc 10!÷7!

Or, 7 = 10−3, d’où la formule qui est plus précisément : 10!÷(10-3)! Le 10 étant le nombre de chiffres sur chaque disque et 3 étant le nombre de disques. On retrouve notre formule générale, avec des factorielles :

Où :

• N est le nombre de disques
• M le nombre de chiffres par disque
• Dans un cas où l’on s’interdit de prendre plusieurs fois le même chiffre.

Cette formule, je ne la connaissais pas par cœur. Je ne la connais toujours pas par cœur. Mais je la retrouve très facilement.

Cette formule est applicable quand on fait ce qu’on appelle un tirage sans remise.

C’est à dire que l’on tire un élément d’un ensemble (par exemple le premier chiffre parmi un ensemble de 10 chiffres), sans la remettre dans l’ensemble pour les tirages suivants. De plus ici, l’ordre a une importance : le tirage {1,2,0} est différent de {2,0,1} par exemple. Le tiercé dans l’ordre aux courses de chevaux est un exemple où l’on pourra employer ceci.

C’est donc différent du Loto. Au Loto, l’ordre n’est pas important. Le tirage {1,2,3,4,5} a autant de valeur que le tirage {3,5,2,4,1} ou encore {5,4,1,2,3}. Autrement dit, on a davantage de chances de gagner que s’il fallait trouver le bon ordre, en plus des bons chiffres.
Pour le loto, avec 5 boules, on a 5×4×3×2×1 façons de les arranger, soit 5! = 120 arrangements, ayant tous la même estime pour la Française des Jeux.

La formule précédente qui donne le nombre de possibilités différentes de tirages sans remise mais ordonnés est donc à diviser par 5!, et l’on aura la formule qui donne le nombre de possibilités différentes de tirages sans remise et sans ordre.

Autrement dit :

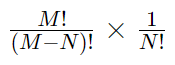
Ou

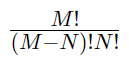
La voici donc, la formule avec les factorielles, retrouvée assez facilement et sans aide.

Ainsi, pour le loto, le nombre de possibilités pour un tirage de 5 boules parmi 49 valeurs est 49!÷((49-5)!×5!), soit 1 906 884 possibilités de tirages. En d’autres termes, on a une chance sur 1 906 884 de gagner.
Si l’on devait tenir compte de l’ordre, on aurait 120 fois plus de possibilités, et donc d’autant moins de chances de gagner. La probabilité deviendrait alors une chance sur 228 826 080.

Et si l’on voulait enseigner quelque chose, c’est ce type de raisonnement qu’on chercherait à faire apprendre et à ressortir lors d’un contrôle.

Pas juste la formule toute prête suivie de quatre ou cinq applications numériques. Une application numérique, c’est juste un exemple d’utilisation d’une formule. Mais retrouver la formule elle-même, y compris si c’est petit à petit, ça c’est démontrer que l’on a compris quelque chose. Ça c’est quelque chose de beaucoup plus important, et de bien moins courant.